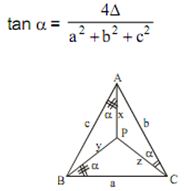
Solution:
Solution
Let there exist a unique point P ...........We have
x2 = z2 + b2–2bz cos α
[By cosine rule]
y2 = x2 + c2–2cx cos α
z2 = y2 +a2 – 2ay cos α
On adding, we get 2( cx + ay + bz) cos α = a2 + b2+ c2 ...........(1)
Also area of DABC =area (DPAB) + area (DPBC) + area (D PAC)
=>D= 1/2( cx + bz + ay)sin α ....(2)
From (1) and (2) ,
We get